hello दोस्तों! इस पोस्ट में आज आप पढेंगे कि कंप्यूटर ग्राफ़िक्स में what is reflection and shearing in hindi. तो चलिए शुरू करते है.
- Reflection And Shearing In Computer Graphics Program Using
- Reflection And Shearing In Computer Graphics Program
अनुक्रम (contents)
About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How YouTube works Test new features Press Copyright Contact us Creators. 2D Shearing in Computer Graphics. 2D Shearing is an ideal technique to change the shape of an existing object in a two dimensional plane. In a two dimensional plane, the object size can be changed along X direction as well as Y direction. Consider a point object O has to be sheared in a 2D plane. Reflection refers to the mirror image of the original graphical object. It is an 180 o rotation operation. Reflection can be done about following ways: x-axis; y-axis; the origin and; A plane perpendicular to the origin; Shearing. Shearing is a transformation in which the shape of the object is slanted about the axis.
If user choose reflection then rotate the triangle in 1800 at (x2, y2) and draw the rotated triangle (which is reflected triangle). If user choose shearing then get the shear value and draw the sheared triangle in the following coordinates (x1, y1, x2+x, y2, x3, y3).
Reflection and Shearing in hindi

Computer graphics में जो तीन मुख्य transformation है वह scaling, rotation, और translation है. इन तीनो का प्रयोग बहुत ज्यादा किया जाता है तथा ये बहुत ही उपयोगी भी है. इनके अलावा भी transformations है जो अन्य applications में उपयोगी होती है. ये transformations है- reflection और shearing.
Reflection in hindi
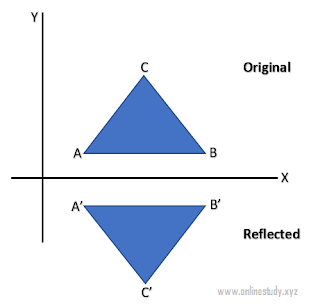
reflection जो है वह original object की mirror image होती है. दूसरे शब्दों में कहें तो यह 180 degree में rotation operation होता है.
reflection transmission में object का size नहीं बदलता है.
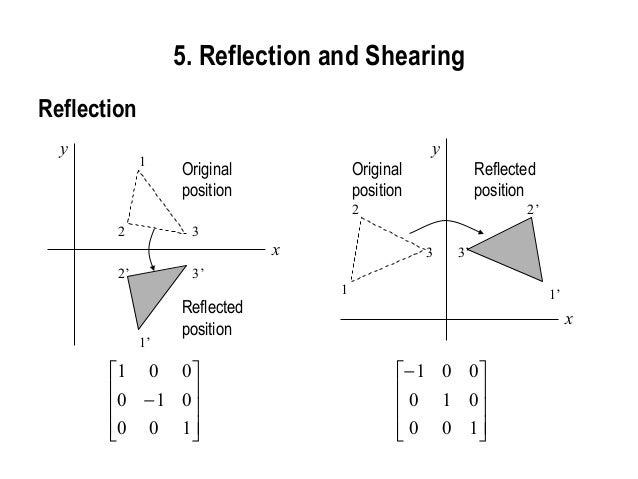
नीचे चित्र में x तथा y axes और इसके origin के साथ reflection को दिखाया गया है.

Shear in hindi

वह transformation जो object की shape को slant (तिरझा) कर दे उसे shear transformation कहते है. shear transformation दो प्रकार का होता है:- X-shear और Y-shear.
इसमें एक x coordinates की value को shift करता है जबकि दूसरा y coordinates की value को shift करता है. हालांकि दोनों cases में केवल एक coordinate ही अपने coordinates को change करता है और दूसरा अपनी value को change नहीं करता है.
shearing को skewing भी कहते है.
X-shear
X-shear जो है वह X coordinates में changes करता है और Y coordinate में changes नही करता. जिसके कारण vertical lines बायीं या दायीं तरफ झुक जाती है जैसा कि नीचे चित्र में दिखाया गया है.
X-shear की transformation matrix को नीचे प्रदर्शित किया गया है.
Reflection And Shearing In Computer Graphics Program Using
Y-shear
Y-shear जो है वह X coordinates में बदलाव करता है और Y coordinate में बदलाव नही करता. जिसकी वजह से horizontal lines ऐसी lines में transform हो जाती है जो कि उपर तथा नीचे की तरफ झुकी हुई होती है. जैसा कि आप नीचे चित्र में देख सकते है.
Y-shear को निम्नलिखित matrix के द्वारा represent किया जाता है.
निवेदन:- अगर आपको यह पोस्ट अच्छी लगी हो तो इसे अपने दोस्तों के साथ share कीजिये और आपके इस पोस्ट को लेकर कोई questions है तो comment के द्वारा जरुर बताएं. धन्यवाद.
Reflection And Shearing In Computer Graphics Program
Related
#include<iostream>
#include<conio.h>
#include<graphics.h>
#include<math.h>
using namespace std;
voiddisp(intn,float c[][3]){
floatmaxx,maxy;
inti;
maxx=getmaxx();
maxy=getmaxy();
maxx=maxx/2;
maxy=maxy/2;
i=0;
while(i<n-1){
line(maxx+c[i][0],maxy-c[i][1],maxx+c[i+1][0],maxy-c[i+1][1]);
i++; }
i=n-1;
line(maxx+c[i][0],maxy-c[i][1],maxx+c[0][0],maxy-c[0][1]);
setcolor(GREEN);
line(0,maxy,maxx*2,maxy);
line(maxx,0,maxx,maxy*2);
setcolor(WHITE);}
void mul(intn,float b[][3],float c[][3],float a[][3]){
inti,j,k;
for(i=0;i<n;i++)
for(j=0;j<3;j++)
a[i][j]=0;
for(i=0;i<n;i++)
for(j=0;j<3;j++)
for(k=0;k<3;k++) {
a[i][j]=a[i][j]+(c[i][k]*b[k][j]); }}
void translation(intn,float c[][3],float tx,floatty){
inti;
for(i=0;i<n;i++) {
c[i][0]=c[i][0]+tx;
c[i][1]=c[i][1]+ty; }}
void scaling(intn,float c[][3],float sx,floatsy){
float b[10][3],a[10][3];
inti,j;
for(j=0;j<3;j++)
b[i][j]=0;
b[0][0]=sx;
b[1][1]=sy;
b[2][2]=1;
mul(n,b,c,a);
setcolor(RED);
disp(n,a);}
void rotation(intn,float c[][3],float ra){
inti=0,j;
float b[10][3],xp,yp,a[10][3];
xp=c[0][0];
yp=c[0][1];
for(i=0;i<3;i++)
for(j=0;j<3;j++)
b[i][j]=0;
b[0][0]=b[1][1]=cos(ra*3.14/180);
b[0][1]=sin(ra*3.14/180);
b[1][0]=-sin(ra*3.14/180);;
b[2][0]=(-xp*cos(ra*3.14/180))+(yp*sin(ra*3.14/180))+xp;
b[2][1]=(-xp*sin(ra*3.14/180))-(yp*cos(ra*3.14/180))+yp;
b[2][2]=1;
mul(n,b,c,a);
setcolor(RED);
disp(n,a);}
voidrefthx(intn,float c[][3]){
inti=0,j;
float b[10][3],a[10][3];
for(i=0;i<3;i++)
for(j=0;j<3;j++)
b[i][j]=0;
b[0][0]=b[2][2]=1;
b[1][1]=-1;
mul(n,b,c,a);
setcolor(RED);
disp(n,a);}
voidrefthy(intn,float c[][3]){
inti=0,j;
float b[10][3],a[10][3];
for(i=0;i<3;i++)
for(j=0;j<3;j++)
b[i][j]=0;
b[1][1]=b[2][2]=1;
b[0][0]=-1;
mul(n,b,c,a);
setcolor(RED);
disp(n,a);}
voidreforg(intn,float c[][3]){
inti=0,j;
float b[10][3],a[10][3];
for(i=0;i<3;i++)
for(j=0;j<3;j++)
b[i][j]=0;
b[0][0]=b[1][1]=-1;
b[2][2]=1;
mul(n,b,c,a);
setcolor(RED);
disp(n,a);}
voidrefthyx(intn,float c[][3]){
inti=0,j;
float b[10][3],a[10][3];
for(i=0;i<3;i++)
for(j=0;j<3;j++)
b[i][j]=0;
b[0][1]=b[1][0]=b[2][2]=1;
mul(n,b,c,a);
setcolor(RED);
disp(n,a);}
voidrefthynegx(intn,float c[][3]){
inti=0,j;
float b[10][3],a[10][3];
for(i=0;i<3;i++)
for(j=0;j<3;j++)
b[i][j]=0;
b[0][1]=b[1][0]=-1;
b[2][2]=1;
mul(n,b,c,a);
setcolor(RED);
disp(n,a);}
voidshearx(intn,float c[][3],float shx){
inti=0,j;
float b[10][3],a[10][3];
for(i=0;i<3;i++)
for(j=0;j<3;j++)
b[i][j]=0;
b[0][0]=b[1][1]=b[2][2]=1;
b[1][0]=shx;
mul(n,b,c,a);
setcolor(RED);
disp(n,a);}
voidsheary(intn,float c[][3],float shy){
inti=0,j;
float b[10][3],a[10][3];
for(i=0;i<3;i++)
for(j=0;j<3;j++)
b[i][j]=0;
b[0][0]=b[1][1]=b[2][2]=1;
b[0][1]=shy;
mul(n,b,c,a);
setcolor(RED);
disp(n,a);}
int main(){
inti,j,k,cho,n,gd=DETECT,gm;
float c[10][3],tx,ty,sx,sy,ra;
initgraph(&gd,&gm,” “);
cout<<“Enter no. of vertices”;
cin>>n;
for (i=0;i<n;i++) {
cout<<“Enter coordinates of vertex”,i+1;
cin>>c[i][0]>>c[i][1];
c[i][2]=1; }
do {
cleardevice();
cout<<“ntt ——MENU——“;
cout<<“ntt 1)Translation”;
cout<<“ntt 2)Scaling”;
cout<<“ntt 3)Rotation”;
cout<<“ntt 4)Reflection”;
cout<<“ntt 5)Shear”;
cout<<“ntt 6)EXIT”;
cout<<“nt Enter your Choice”;
cin>>cho;
switch(cho) {
case 1:
cout<<“nt Enter translation factor for X and Y axis:t”;
cin>>tx>>ty;
cleardevice();
setcolor(15);
disp(n,c);
translation(n,c,tx,ty);
setcolor(15);
disp(n,c);
getch();
break;
case 2:
cout<<“nt Enter scaling factor for X and Y axis:t”;
cin>>sx>>sy;
cleardevice();
setcolor(15);
disp(n,c);
scaling(n,c,sx,sy);
getch();
break;
case 3:
cout<<“nt Enter rotation factor :t”;
cin>>ra;
cleardevice();
disp(n,c);
rotation(n,c,ra);
getch();
break;
case 4:
intch;
do{
cleardevice();
cout<<“ntt ——MENU——“;
cout<<“ntt 1)Reflection about x axis”;
cout<<“ntt 2)Reflection about x axis”;
cout<<“ntt 3)Reflection about origin”;
cout<<“ntt 4)Reflection about the line y=x”;
cout<<“ntt 4)Reflection about the line y=-x”;
cout<<“nt Enter your Choice”;
cin>>ch;
switch(ch){
case 1:
cleardevice();
setcolor(15);
disp(n,c);
refthx(n,c);
getch();
break;
case 2:
cleardevice();
setcolor(15);
disp(n,c);
refthy(n,c);
getch();
break;
case 3:
cleardevice();
setcolor(15);
disp(n,c);
reforg(n,c);
getch();
break;
case 4:
cleardevice();
setcolor(15);
disp(n,c);
refthyx(n,c);
getch();
break;
case 5:
cleardevice();
setcolor(15);
disp(n,c);
refthynegx(n,c);
getch();
break;
default:
cout<<“nt Invalid Choice !!!”;
break; } }
while(cho!=5);
case 5:
int cha;
floatshx,shy;
do {
cleardevice();
cout<<“ntt ——MENU——“;
cout<<“ntt 1)X-shear”;
cout<<“ntt 2)Y-shear”;
cout<<“nt Enter your Choice”;
cin>>cha;
switch(cha) {
case 1:
cout<<“nt Enter Shear factor: “;
cin>>shx;
cleardevice();
setcolor(15);
disp(n,c);
shearx(n,c,shx);
getch();
break;
case 2:
cout<<“nt Enter Shear factor: “;
cin>>shy;
cleardevice();
setcolor(15);
disp(n,c);
shearx(n,c,shy);
getch();
break;
default:
cout<<“nt Invalid Choice !!!”;
break; } }
while(cho!=2);
case 6:
exit(0);
break;
default:
cout<<“nt Invalid Choice !!!”;
break; } }
while(cho!=6);
getch();
closegraph();}